Let's explore an indexing structure called Vantage Point Tree, understand it intuitively, mathematically and test time complexity of a simple implementation in python
We will start very gently, talking about search in general - feel free to skip this section

We search all the time

Search algorithms are being used daily and everywhere. You wake up, and you search for the t-shirt you feel like wearing today. Then you search for your car keys because a sapless location of your keys is not something emotionally and worth remembering. You turn on your phone and search for a cafe to have breakfast at, utilizing dozens of searches while you are searching - your file system, DNS, search engine, tracking IDs of your device, etc...

Search, Big-O, and linear search

The key concept in a search problem is that you don't want to go through the whole pool of objects when looking for some subset / specific element. Such a search is called linear and is not very effective. We can measure its time-complexity with Big-O notation - capturing how many operations (decisions) we have to do in the worst case until we find what we are looking for. With a linear search, it's \(O(N)\) (number of items)

Imagine yourself looking for your keys in a backpack with just one pocket. You take an item from the backpack and ask: "is it my lost key ?" and if not, throw it away. The worst-case (that's what Big-O notation denotes) is that you have to throw away everything else until the only object remaining in the backpack is your lost keys

Indexing structures, binary trees

There are many ways how to store stuff so you can later find it. Most of the techniques work in a similar way - sort things before searching either in batch or dynamically every time we want to store an object

One (of many) ways how to do it is binary search tree. You can express some parameter of your object with a number - it can be a length of text, a height of a person, rating of a restaurant - anything you would like to search in future. Let's say the numbers are \(1,3,8,7,15,5,2\)

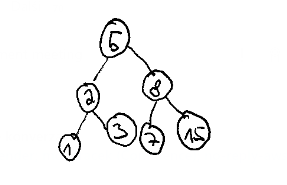
Let's say you want to find data about the product with id \(7\):

Is \(7 > 5\) ? Yes ! -> Go right
Is \(7 > 8\) ? No ! -> Go left
We arrived at 7, we can
- Tell "yes, there is record with ID 7"
- Load more data about record 7 (as location on disk/cluster is stored in index)

Let's how many comparisons we can save by searching through a pool of ... let's say of 100 items?

While there are many more structures, each suitable for different use-case (for example, bloom-filter can tell about (non)presence of an item in a pool with \(O(1)\) - constant complexity and sub-linear space complexity) Binary search trees and it's variants such as b+tree are very powerful as they guarantee that its time complexity is \(O(log_2(N))\), and they can perform range-scans That's the reason why these indexes are used by almost all databases for decades.

K-nearest neighbors, range inclusion test

So with all these fancy structures, why do we need something else?

Let's say you have a picture of a person and you would like to find the 5 most similar faces or faces, which are similar enough, that you can assume it's the same person.
You can describe features (such as distance between eyes) with some number and find pictures of people with a similar value. You can even encode multiple features and use a compound index (still utilizing b-tree) to find similar faces

The problem arises when you have thousands of these features. A compound index will first encode the first feature, then splits leaves with the same value of the first feature based on the second feature and so on

So:

Order of features matters - features have to be ordered by the "quality of split" (for example, computed with gini gain)
It's not always easy to describe an object with a relatively small number of indexable features (which also maximizes between-class covariance so you can tell objects apart by using the features)

This is something metric space can help with

Metric spaces

In metric space, unlike vector space objects are not identified by their coordinates. Each object is identified by it's distance to other objects. By the distance we mean any metric distance function - it can be euclidean distance or even prediction of similarity from some trained model

(A bit) formal definition

Metric space is a tuple of \((M, d)\) where

\(M\) denotes some set of objects (for example faces)
\(d\) is distance function \(M \times M \rightarrow \mathbb{R}\) mapping any tuple of objects to real number - their distance

There are the following axioms:

"identity of indiscernibles" \(d(x, y) = 0 \iff x = y\) ("two people don't have same face, each person has only one face")
"symmetry" \(d(x, y) = d(x, y)\) "NYC has the same distance to San Francisco as San Francisco to New York"
"Triangle inequality" \(d(x, z) \leq d(x, y) + d(y, z)\) "There are no magical shortcuts"

Identity of indiscernibles

This is self-explanatory and rarely poses an issue if we want to use metric spaces for something

Symmetry

Some problems have asymmetric distance. For example, there might be one-way traffic if we talk about the distance between places on a map

There is an easy work-around how to turn asymetric distance to symetric one:

\(d_{\text{sym}}(x, y) = d_{\text{asym}}(y, x) + d_{\text{asym}}(x, y)\)

Triangle inequality

This essentially means "direct route is never worse than detour". It's impossible to construct a triangle if this property does not hold.

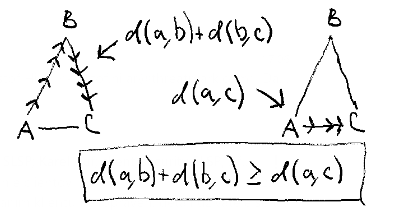
This property is extremely important in data structures able to index metric spaces as it's capable of pruning possible points and therefore limiting number of invocations of distance function

It's possible to convert a non-metric distance function (distance function not respecting triangle inequality property) to a metric function by making it more convex. Let's leave this for later

Searching metric spaces

There are two kinds of searches usually done in metric space:

Range scan \(\{ o \in X, d(o,q) \leq r\}\) "give me faces similar enough to this one"
K-nearest neighbors search \(\{R \subseteq X, |R|=k \wedge \forall x \in R, y \in X -R:d(q,x) \leq d(q,y)\}\) "give me k most similar faces"

Again, we could naively compare the picture of a face we have taken with all the faces we have in the database, but we don't want to do it as the distance function is expensive

We have to load the face picture / features from some disk - performing a slow operation on a block device
We have to invoke the function, eating CPU time (e.g. CNN ANN)

We need to minimize the number of times we use the distance function we have to ensure, that number of required calls for \(d\) grows slower than \(N\) (size of dataset)

Vantage Point Trees

Vantage Point Tree is a data structure, which can perform searches in \(O(log_2(N))\) complexity

Indexing

(A bit) format definition is as follows:

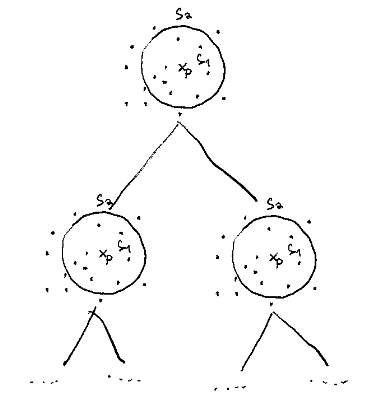
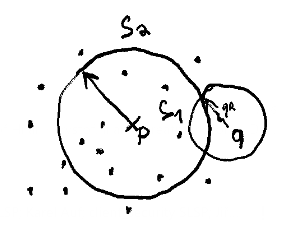
We take a point \(p \in X\) and promote it to a pivot, called "Vantage Point" by author of original paper
We choose radius \(r\) such that it's median of \(d(o\in X, p)\)
We divide the set into
- \(S_1 = \{o \in X | d(o,p) \leq r \}\)
- \(S_2 = \{o \in X | d(o,p) \gt r \}\)
Recursivey repeat with both \(S_1\) and \(S_2\)

So what does it mean?

We recursively divide space into smaller (n-dimensional circular areas) / "balls" each time using \(r\) which is the median of distances of undivided points to a pivot. Median means, that half of the points will have \(d(o, p) \lt r\) and half \(d(o, p) \gt r\), in another words: "It will be balanced binary tree !"

Searching

Range scan

We want to find all points \(o \in S\) in search radius \(qr\) from point \(q\) (or in another words \(o \in S | d(q, o) \leq qr\))

Look at a root of tree and find first pivot point (first split)
Compute distance \(d(q, p)\)
If \(d(q, p) \leq qr\), include the point

Now the most important part: Decide if we should include left or right branch

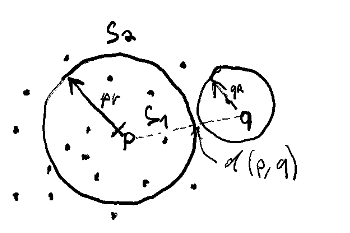
A: \(d(p, q) - pr \gt qr \implies \forall o \in S_1, d(q, o) > qr\)

Let's rephrase it:
- If we take distance from query to pivot and subtract radius around the pivot, no point will be closer than this distance
- If the pivot is so far from the the query, that even the most optimistic point (subtracting radius of pivot) is too far, we can ignore these points
B: pt - \(d(p, q) \leq qr \implies \forall o \in S_2, d(q, o) \leq qr\)

Let's rephrase it: * If the pivot is so close to query, such that whole search radius is inside pivot radius, we can take all the points
C:

In this case, we have to visit both branches

Python implementation

We have recently found a use-case for a search similar to this in ThreatMark, unfortunately I can't tell you more about it :)
After testing several alternatives, I find this implementation on github most readable and sane

So, ... we had some millions of some objects and trained ANN to tell how similar they are.
The script used an ugly global variable comparison_count to count the number of executions of this function

We had to deal with several issues:

The function is not symetric, we use mentioned work around \(d_{\text{sym}}(x, y) = d_{\text{asym}}(y, x) + d_{\text{asym}}(x, y)\)
The function does not respect triangle inequality, we had to make the function more convex by using a square root of the distance function

def distance(a, b):
    global comparison_count
    comparison_count += 1

    if a == b:
        # Axiom of metric spaces
        return 0

    epsilon = 1e-12 # If a!=b, then result must be nonzero
    return 2-(model(a, b)[0] + model(b, a)[0]) + epsilon

def convex_distance(a, b):
    return np.sqrt(distance(a, b))

Then we just tested both performance and correctness with several scripts (simplified, reducted)

search_complexity = []
comparison_count = 0

# set k value (k-nearest-neighbours)
top_k = 10

# Perform the k-nearest search for 10 different objects, average the result
queries = random.choices(ids, k=10)

sizes = [10, 20, 100, 500, 1000, 2000, 10000, 20000, 50000, 100000, len(pool)]
for pool_size in sizes:
    print("Searching with size:", pool_size)

    # Build the tree from scratch
    tree = vptree.VPTree(ids[:pool_size], distance)

    counts = []
    for query in queries:
        comparison_count = 0
        for k, result in enumerate(tree.get_n_nearest_neighbors(query, top_k)):
            if k>= top_k:
                break

        counts.append(comparison_count)

    avg_count = np.mean(counts)
    search_complexity.append([pool_size, avg_count])

And it turned out that it scales!

Conclusion

Metric spaces might be a good option how to search in a pool of high dimensional objects and a Vantage Point Tree is a very simple, but powerfull data structure

When thinking about using that for your project, consider at least the following:

Metric space requires an symmetric distance function
Metric space has triangle inequality axiom (you can bypass that limitation/decrease effects(=invalid search results) by making the function more convex)
VPT does not describe how to handle edits and how to rebalance it (naive inserts lead to degradation) you have to use some extension of VPT to solve that
Choosing a pivot has an impact on the performance of the algorithm. Usually, the pivot is chosen either randomly or as a statistical outlier

If you read so far, I would like to thank you
If you found any issues in this post, please let me know!