Let's re-discover what is logistic regression, why and how it works.
I will assume that reader can sum or multiply two numbers and nothing more, we'll discover the rest :)
Why am I writing this ?
It's the step 2 (teach) and step 3 (find gaps) and step 4 (simplify) in the famous Feyman's technique

“If you can’t explain it to a six-year-old, you don’t understand it yourself.”
Albert Einstein

Why about logistic regression ?
Besides all the hype "cool models" get, logistic regression is still a very powerfull model and is a "gateway" to deep learning ("the cool stuff") - if you deeply understand logistic regression, you understand 90% of neural networks (as a single neuron is logistic regression).

Classification

The mayor of Hobbiton has heard about machine learning and would like to give it a try
He would like to know if there is still potential in Hobbits in the 21st century
He immediately collects a dataset (=numbers describing some readings).
For each young hobbit, he collects the size of his foot and the number of other hobbits he can lift on a benchpress
Besides that, he also has for every person knowledge if he is a hero (like Frodo, Sam, Bilbo)

He hopes to build a model (a simplified representation of reality) to:

• Understand which of the measurements (foot size, strength) correlates more (is a better predictor of) the hero status
• Based on the measurements, predict if he will become a hero (like Mr. Frodo)

Let's visualize the problem:

• Each point represents one Hobbit
• Green color means that he is a hero, red color means that he is not
• X coordinate (horizontal) of point is \(x_1\) (size of his foot) and Y coordinate (vertical) is \(x_2\) (# of hobbits he can lift). So the leftmost green point - his foot is size 1.5, and he can lift 4 Hobbits on a benchpress

The black line is the so-called decision boundary. It can have different shapes, but for logistic regression (without tweaks) it's a line, or if we add more dimensions (plane/hyperplane).

Please play with it and place the line so it separates the green from the red (heroes from non-heroes)
Are you done ?

You have probably arrived at something like (or maybe something slightly different):

• Intercept: 3
• Slope: -0.4

You have just trained your first machine learning model (in a manual way :)) !

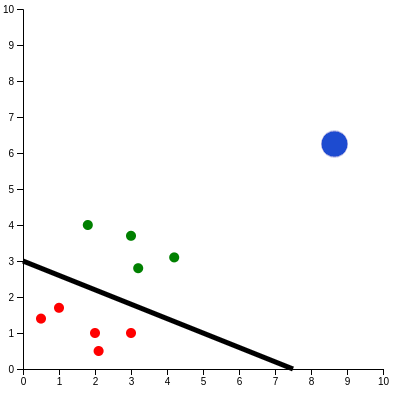
But what if we add a new point (the blue one) ?
It's way outside the data we have seen (stronger than any other Hobbit, incl. Sam).
Because it's on the side of decision boundary of "greens", our prediction will be "hero".
Also, because it's much further from decision boundary (higher scores), we will be more confident about success of this Hobbit than others (green)
We call this \(\hat{y}\) (pronounced "y hat") and it's the output of the model, given some inputs

We can interprent the \(\hat{y}\) as probability of class being "true" ("true" = hero, "false" = not-a-hero in our case)
It's denoted like this:

• \(p(y=1|x,\text{model}) = \hat{y}\)
• \(p(y=0|x,\text{model}) = 1-\hat{y}\)

It's read as "probability, that y is 1, given our trained model and input is y hat".

What does it mean ?
Let's say, the output is \(0.85\). In case the model is calibrated (feel free to deep dive into that), it follows that:
If I see 100x Hobbits with \(\hat{y}\) of 0.85, 85 out of these 100 will be heroes (like Mr.Frodo)

Because Hobbit either becomes hero or not, there are only two outcomes (binary classification problem), therefore \(p(y=1|x,\text{model}) + p(y=0|x,\text{model}) = 1\) - this is 2nd axiom of probability ("if you know everything what can happen, something from what can happen will definetelly happen")

Let's recap

Time for small recap and a bit of notation

• Classification is one of types of ML tasks, goal is to predict class of unseen samples
• The dataset is a set of \(x\)'s (inputs) and \(y\)'s (expected outputs)
• We can have one or thousand inputs, we denote them \(x_1, x_2, \dots x_n\)
• The output of classifier is denoted \(\hat{y}\) and is often probabilistic

Hypothesis

In machine learning, hypothesis is our believe how the data will look like (an equation). For example in logistic regression (without tricks), we assume the data can be split by a line/plane/hyperplane and we need to find (=train) the parameters (where is the line)

There is so-called bias-variance trade-off it states, that you have to choose (no free meals)

• High bias - We have very strong restrictions on "shape" of data. For example we assume it's along a line. If it's too strict we might not understand the data - the model is not complex enough to capture the data. This is called underfit
• High variance - We don't have any assumptions, we accept any "shape" of data. We might perfectly describe the data on the training set, but the model can be totaly useless with the data it did not see during training. Imagine a point far right outside your notebook - I have no idea what this crazy function (rightmost "overfit") will predict. This is called overfit

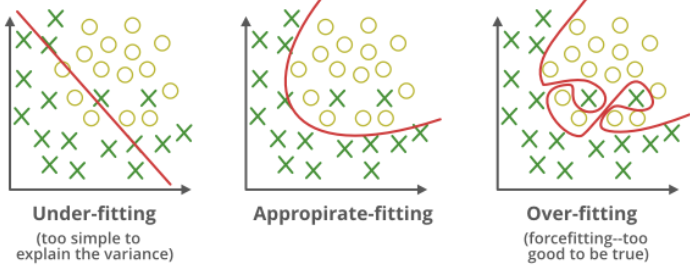
The logistic regression we will deep-dive now is on extreme side of "high bias, low variance" - the model is very hard to break (overfit), however it might not "capture the essence" of very hard problems

Hypothesis - logistic regression

Remember how you trained the model a minute ago ?

You have described a line with intercept and slope

\(y = \text{intercept} + x \times \text{slope}\)

This means: "If I want to know y coordinate, I need to take intercept, and for each unit of x also add slope"
Extreme cases:

• \(\text{intercept}=3, \text{slope}=0\) -> What ever I throw in as X, the output (y) is always 3
• \(\text{intercept}=0, \text{slope}=-2\) -> For each X I throw in, I remove 2 from the output (y)

Please "train" the model again

I would expect something like:

• \(w_0 = -4.7\)
• \(w_1 = 1\)
• \(w_2 = 1\)

It turn's out, we can describe line (plane/hyperplane) in more ways.
This time it's equation \(w_0 + w_1 \times x_1 + w_2 \times x_2 = 0\)
If we just subtract \(w_0\) from both sides we get: \(w_1 \times x_1 + w_2 \times x_2 = -w_0\)

With our values, it's: \(x_1 + x_2 = 4.7\)

Imagine all the possible points on the grid, only the ones, where if you sum their coordinates and you get 4.7 will be part of line (yes, the line is infinite). Let this sink.

You can of course have more than two input features. The decision boundary is then

\(w_0 + w_1 \times x_1 + w_2 \times x_2 + \dots + w_n \times x_n = 0\) which is equivalent to
\(w_0 + \sum_{i=1}^n[w_i \times x_i] = 0\) (you have up to \(n\) features)

What is it ? \(\sum\) is a greek letter "sigma" and stands for summation - we sum everything inside the brackets. If there are variable with index, we go from what's on the bottom (\(i=1\)) up to what's on the top (\(n\)) - in this case from feature 1 up to feature \(n\)
\(\sum_{i=1}^n[w_i \times x_i] = w_1 \times x_1 + w_2 \times x_2 + \dots + w_n \times x_n\), it's just more "compact"

Small detour - linear algebra

We have lot's of \(x\)'s and \(w\)'s, leading to lot of multiplications and sums
We need to drill lot of holes, let's get an electric drill :)

Let me introduce you a vector:

It's just collection of numbers - we can talk about the whole collection instead of individual ones !
We denote vector with little arrow \(\vec{v}\) to know, that it's not a number (called scalar - like scaling something)
The first vector is \(\vec{x}\), representing a single sample (=1 Hobbit with multiple measurements - like size of foot)
The second vector is \(\vec{\theta}\) "theta", representing all the parameters we need to place a line in space to tell heroes and ordinary Hobbits apart
The vectors had shape (n x 1) (n rows and one column)
Let's make transpose

Now we have row vectors, the shape is (1 x n) (1 row and n columns)

Let's play with the objects :)

This is scalar multiplication

This is dot product or inner product
It's also special case of matrix-multiplication (1 x n times n x 1 matrix)
Matrix is just vectors stacked, no worry, no Orcs here

Each row is one Hobbit (multiple measurements), each column is same type of measurement of different Hobbits. \(X_j^{(i)}\) is \(j\)'th feature of \(i\)'th Hobbit

This result is a m x 1 matrix (=column vector), where each row is dot product of the inputs for that user (scores) and parameters/weights
Please note, that you cannot change order of matrices as you wish (we say that multiplication is not commutative).

Back to decision boundary

So originally we had \(w_0 + w_1 \times x_1 + w_2 \times x_2 + \dots + w_n \times x_n = w_0 + \sum_{i=1}^n[w_i \times x_i] = 0\)
The \(w_0\) is messing up the nice sum of products (product is just fancy word for multiplication)
If we make \(x\) a vector \(\vec{x}\) and prefix it with number 1 (so \(1 \times w_0\) is part of the sum), we might neatly use dot product :)

So now we know how to describe the decision boundary with any number of dimensions (=input features/readings)

Hypothesis - revisited

Our decision boundary is \(\vec{\theta}^\intercal \cdot \vec{x}\).
The decision boundary is equation, assign any possible point some number

The more green the area, the higher is the number, the more red it is, the lower it is

Is this our hypothesis ? Do we simple return \(\vec{\theta}^\intercal \cdot \vec{x}\) as \(\hat{y}\) ?
Not quite - if do this, our result could be arbitrary real number
Imagine Hobbit getting 10 points on both features (10 size foot, 10 Hobbits lifted on benchpress) -> \(-4.7 + 10 + 10\) is definetely not a probabilistic value
We need to somehow confine the output to return probabilistic output (\([0, 1]\))

I want you to meet a new friend, let's call him sigmoid or logistic function

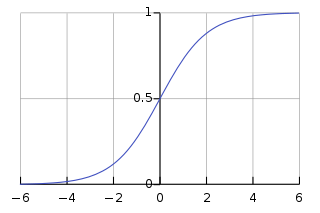
It's a growing function, mapping infinite range into \([0, 1]\) interval.
What does it mean ?

• On X axis (horizontal) you pick any point (=input)
• On Y axis (vertical) you will find the output

The equation of function is

where \(z\) is the name of input

The function was invented by many people, it's mostly attributed to Pierre Verhulst who used it to model growth of population. In his theory, there are three stages described by the S curve:

• Lag phase (not too many organisms to reproduce)
• Growth phase (exponential growth)
• Diminishing growth phase (limited resources)

We divide number one by a increasingly larger number - it cannot be more than one and one it's at infinity
The \(e\) (euler's number) is inverted \(\frac{1}{e^z}\) - this is what makes the S shape
If we throw in \(z=0\), we get \(e^0=1\), therefore we divide \(1\) with \(2\) - the result is 0.5 (=model does not know, it's a coin toss)

This is the perfect function to turn our output (high green numbers, low red numbers) into interval \([0, 1]\)

Our hypothesis is therefore

Or if we want to predict multiple samples (each of multiple readings), we can use matrix multiplication:

When we train the model (find parameters \(\vec{\theta}\)), we need to prepare ground for the sigmoid:

• The decision boundary equation shall return 0 for points laying on the decision boundary - sigmoid translates those to 0.5 ("I am not sure" - a coin toss).
• The further we are from boundary into the green area, the higher is the input for sigmoid and closer our prediction is to 1.0.
• The further we are from boundary into the red area, the lower is the input for sigmoid and closer our prediction is to 0.0.
  

Congratulations, you can now predict hero status of infinite amount of Hobbits with infinite amount of features using logistic regression !

Cost function

We are now getting closer to the interesting part - how do you train such model ?
How do you find out the best value of \(\vec{\theta}\) ?

There are algorithms we will go deeply into, however before that - assume that you randomly change the parameters or use brute-force, to systematically try all the possible parameters - how do you know, that you've found the best ? How do you objetively judge the quality of a fit ?

We need some function, which will tell us how good/bad our parameters is - this is called loss function or cost function and in general it tells us how "bad" it is.
Can we figure out intuitively some ? Looking at the picture, it could be something like counting number of points of wrong color at each side of decision boundary (red dots in green area, green dots in red area).
Issue with this function is that ignores magnitude of mistakes - let's say the Hobbit kills Smaug, but we have given him only 0.01 probability, that he succeeds. This is bigger error than saying "I don't know" (\(\hat{y} = 0.5\)).
It turns out we need something like this:

• If the true class (\(y\)) is \(1\), we want rapidly descending function (so telling that it's \(0\) is huuuge error)
• If the true class (\(y\)) is \(0\), we want rapidly growing function (so telling that it's \(1\) is huuuge error)

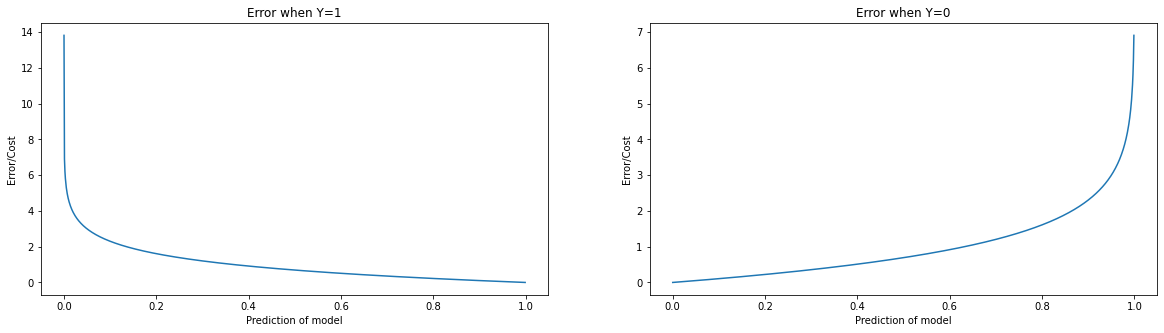
The function above is just inverted logarithm

It's a bit clumpsy, we need single equation, so we can sum up all the errors and know "how bad we are in average", considering all the samples we have. The equation above is just "judging" single sample.

The trick is, that \(y\) can only have values \(\{0, 1\}\) - we can use it:

• \(-y log(h_\theta(x))\) works well if \(y=1\) (turns into \(-1 \cdot log(h_\theta(x))\)) and is harmless if \(y=0\) (multiply by zero)
• \(-(1-y) log(1-h_\theta(x))\) works well if \(y=0\) (turns into \(-1 \cdot log(1-h_\theta(x))\)) and is harmless if \(y=1\) (multiply by zero)

We can get average error by summing error for each sample and dividing by number of samples we have (\(m\)).
We denote such function \(J(\vec{\theta})\) and the "API" is "you give me \(\vec{\theta}\), I tell you how bad it is"

What did we do ?

• We have added together two errors as each of them works for one class and is harmless (returns 0) for other
• We have used "sigma notation" to sum up all the errors (one error for each of \(m\) samples)
• We have taken the \(-\) sign out (subtracting lot of things is same as summing them up and flipping the sign)

We can get rid of the "sigma" by vectorizing the equation. What we do is that we "multiply and then sum it up" - this is exactly what our dot product can do:

What is happening ?

• \(\vec{y}\) is a row vector, we have to transpose it to \(\vec{y}^\intercal\) to get a column vector (=1 x m matrix)
• \(log(h_\theta(X)\) results into a row vector of predictions (=m x 1 matrix)
• Dot product of 1 x m and m x 1 matrix is single number (a 1 x 1 matrix) - each number multiplied by corresponding buddy on ther side and then summed up

Let's take a look at the left part (used to judge class 1)

The result is a single number - sum of individual errors multiplied by the class (if class is 0, we multiply it by 0, because the formula above is just part for when class = 1)
The same thing works for the class 0
Going back to our vectorized equation:

This formula is called log loss or binary cross-entropy - it's a cost function used to measure of fit for a binary classifier (of any type)

Quick recap

• We are doing binary classification, it's a special case of classification, where there are two classes \(y \in \{1, 0\}\)
• We are talking about logistic regression, which is one of many binary classification models
• The model with parameters form a hypothesis
• The hypothesis for logistic regression is \(h_\theta(X) = \frac{1}{1+e^{-X\cdot \vec{\theta}}}\)
  • It's a line/hyperplane somewhere in space (position and orientation determined by \(\vec{\theta})\)
  • Points on the decision boundary get's value 0.5
  • Points in one direction gets higher and higher numbers, asymptoticallly approaching 1
  • Points in other direction gets lower and lower numbers, asymptoticallly approaching 0
• If we pick and \(\vec{\theta}\) we can judge how well the hypothesis works with that (how well does it separate the classes of our traning set)
  • The function is \(J(\vec{\theta}) = \frac{1}{m}[-\vec{y}^\intercal log(h_\theta(X) - (1-\vec{y})^\intercal log(1-h_\theta(X))]\)

What do we miss ?
If we would like to train our model (to get a hypothesis), we would have randomly try out values and ask our cost function how bad it is, maybe taking notes of the best guess and then returning back to it if we cannot find a better one

Fortunatelly, smart people have figured out a way, which guarantees, that:

• We will find the best parameters some day
• At each step, we will get better

Sounds optimistic right ? :)

Optimization

Imagine a landscape, for example piece of Tolkien's Middle-Earth

Let's say that each point represents a value of \(\vec{\theta}\), so

• Left side (the trees): low \(\theta_1\)
• Right side (the fence): High \(\theta_1\)
• Bottom side (the bridge): Low \(\theta_2\)
• Top side (the field): High \(\theta_2\)

Now let's assign each point / pixel another value. The higher the point (altitude), the higher the value. Looking at the picture, points in field will get the highest numbers, while the river will get the lowest numbers, you get me ?
We are talking about \(J(\vec{\theta})\) !

Optimization is simply finding the lowest point (according to cost function) on the landscape.
Different algorithms travel different routes, are suitable for different landscapes, however they have one in common - they have you covered, they will find you nice, little spot somewhere (down) near river and won't guide you to the tower of Isengard :)

If you feel nerdy, you can take a look for example on Newton's Method, or bear with me, we will deep dive into gradient descent

Gradient descent

Gradient descent is primitive, but powerfull.
It works like follows:

• You start somewhere, anywhere (in this case behind the fence)
• Untill you "feel good" (means you find the \(J(\vec{\theta})\) acceptable) or you are stuck (\(J(\vec{\theta})\) is not decreasing):
  • Find a direction down from your current location
  • Jump in the direction

I guess you can imagine some edge cases:

• You jump too much -> you jump ower the river and end up actually higher than before (not good)
• You jump too little -> you will be jumping for a while....

This is where so called learning rate \(\alpha\) (greek "alpha") comes in. It's the size of the jump you do each time - it's configurable and you need to make sure it's not too high or too low

Everything comes up to single thing: If I am about to jump, I change value of \(\vec{\theta}\) in the direction down, by a constant \(\alpha\)

We are working with "direction uphill", this is reason why we subtract it (flip the sign), to get "direction downhill".
The "direction uphill" is the tricky part - to know how to get it, we need to make another detour before going back to Hobbiton

Detour - calculus

Calculus has multiple branches, but one of them is dedicated finding ways downhill - derivatives

The idea is simple:

We have a function - you give it some \(x\) and receive some \(y\) - we say that

• \(x\) is independent variable (you can plug in whatever you want, as long as the output is defined)
• \(y\) is dependent variable (the value of \(y\) depends on what you plug in as a \(x\))

We are intereseted in how steep is the function at each point.
Consider function: \(f(x) = 2x\)

• You give it 2, you get 4
• You give it 5, you get 10
• You give it 0, you get 0

The same goes for difference "delta"
I increase \(x\) by one point, the output is increased by two points:

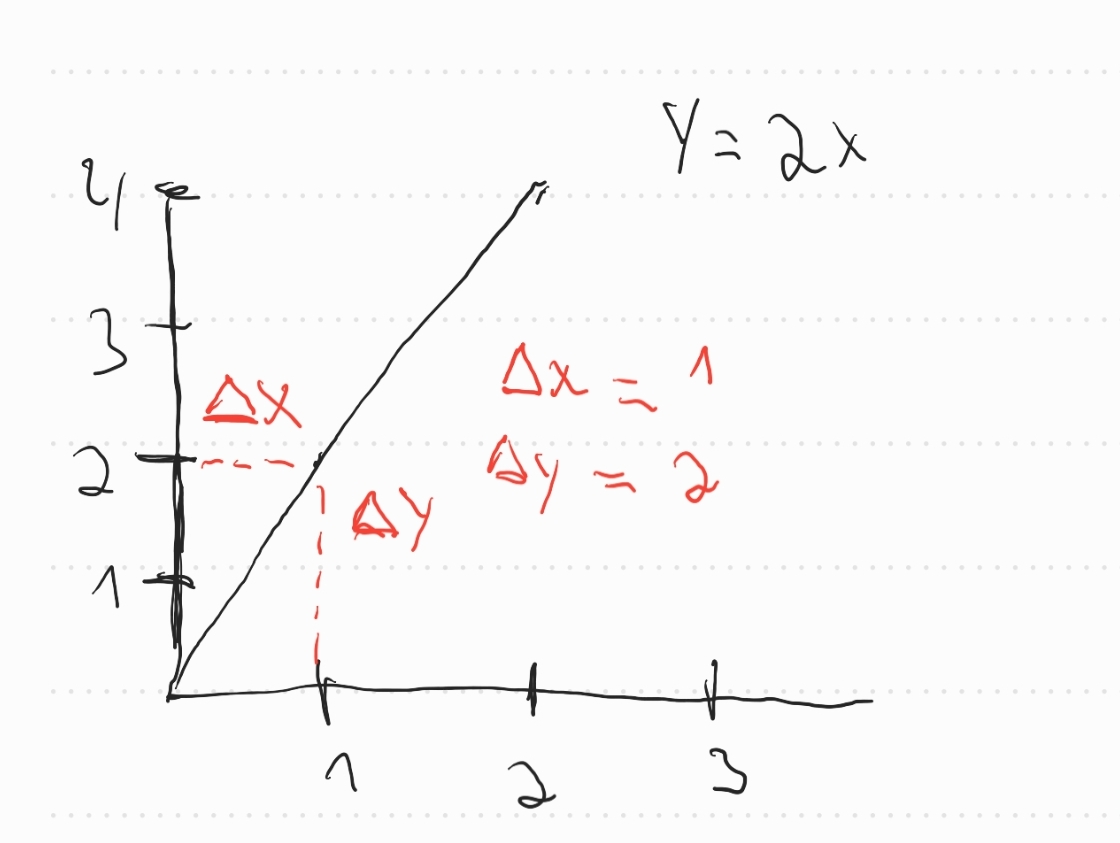
The slope is simply ratio of coordinate deltas:

\(\frac{\delta y}{\delta x} = \frac{2}{1} = 2\)

It's describing "impact on output if I touch the input".
Using this for gradient descent, we know, that at each point, the diretion is "up" with "slope" of 2
If we want to move down, we should better invert it (minus sign) and move back in \(x\), because increasing \(x\) also increases (twofold) the \(y\)
It's just 2D, so the direction is "go left if you want lower \(y\)"

Fancy people call this derivative of function and they argue how to denote it:

• Mr. Leibniz wanted to call it \(\frac{dy}{dx}\)
• Mr. Netwon wanted to call it \(f^{\prime}(x)\)

Here \(dx\) or \(dy\) means "small change of x" or "small change of y"
The "d" stands for "delta", like "difference"
Sometimes greek letter \(\Delta\) (delta) is used for that: \(\frac{\Delta y}{\Delta x}\)

These two guys also argued who invented calculus. As Isaac Newton was president of the Royal Society, he simply decided, that he inveted it first :)
There is also third notation regarding partial derivatives, which will be usefull for us:

This tells us "how is our cost function changed if I touch first parameter \(\theta_1\)"
We will ask same question about \(\theta_1 \dots \theta_n\)
The result will be comperhesive vector of partial derivates, called a gradient

This tells us every parameter and it's impact (direction) on the cost function. If we move in a opposite direction, we are guaranteed to move down a bit !
In our gradient descent, the update rule becomes:

Can we calculate it the same way as with \(f(x) = 2x\) ?
Not yet, we need better tools

In the \(f(x) = 2x\) the function is linear, the derivative (slope) is same everywhere along the line
But what if the function is twisty ?
What if adding \(1\) is too much and we will miss something ?

Let's try it !
This is our sigmoid function

The black line is describing the direction (slope/steepness) of each point. It's called tangent line

We can observe that:

• In different "parts" of function (different \(x\)) the slope/steepness (=ratio of \(\Delta y\) and \(\Delta x\)) is different
• If we "cut" different "piece" of function (from \(x\) to \(x + \Delta x\)), the slope/steepness is also different

So we need another function describing steepness of this function - so we can about each point (\(x\) axis) how steep is it.
One question remains - What change (\(\Delta x\)) is small enough to "understand" the function ?
The two guys figured out, that safe is to use "infinetely small change"

Let's say I have:

• \(x\) arbitrary point (input) of function
• \(h\) a number "infinetelly small"
• \(x + h\) a bit to the right from \(x\), with in a "infinetely small way"

People call this limits

You can interpret it as: "Derivative of function x is ratio of raise (how is y increased) over run (how is x increased) as the increment on input (h) get infinetelly small"
This is it ! This is definition of derivative - with this, you can find slope of any function, with this, you will know how to change inputs so the function output gets smaller / bigger !

Let me give you one bonus: Opposite of differentiation is integration.

Fancy people call this Fundamental theorem of calculus, but it simply means: "If you chop function to small pieces, you can glue it back to get what you got before you chopped it" It's super usefull, but not for us now

While it's possible to use the limit definition of derivative, it's quite painfull.
There are certain kinds of functions and relations, you can "pre-compute" it and then just use it as a template, when computing the derivative of a non-trivial function

Let's start with derivative of polynomial
Polynomial is a function in format \(x^0 + x^1 + x^2 + \dots + x^n\)
So just sum of some powers of \(x\)
Let's take derivative of this \(\frac{df}{dx} [f(x): x^2]\)
Using our limit notation:

Distributing the square (=actually compute \((x+h) \times (x+h)\))

Subtracting \(x^2\)

The nominator is full of \(h\)'s, let's make it explicit

\(\frac{h}{h}\) is 1

As \(h\) is infinetely small, we can just throw it away and use \(2x\)

So, in a function \(x^2\), the slope at any point is \(2x\)

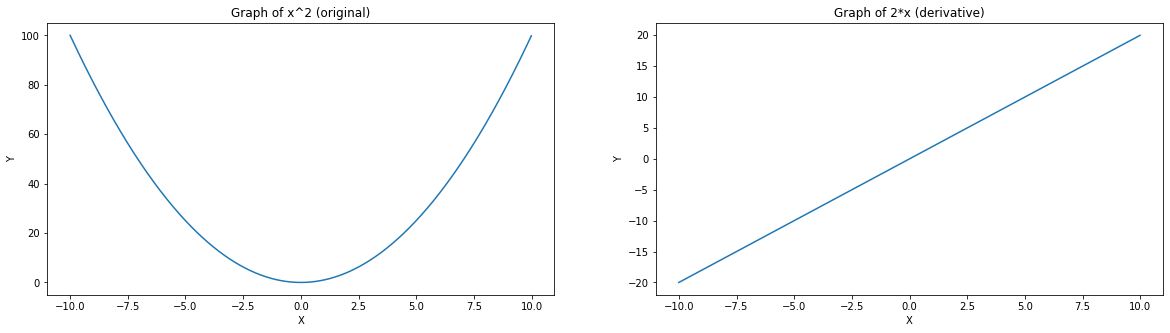
• If you are below zero (e.g. -5), the slope is -10 (going down)
• If you are above zero (e.g. 5), the slope is 10 (going up)
• The further you are from middle, the more steep (either down or up) the function is

The trick is that derivative of \(x^k\) is \(k\times x ^{k-1}\)
So:

• \((x^3)^\prime = 3x^2\)
• \((5)^\prime = (5x^0)^\prime = 0\times5\times x^{-1} = 0\) (derivative of constant is zero)

The last trick is a chain rule

Consider function \(f(g(x))\)

• Function \(f\) depends on output of function \(g\) at point \(x\)

We want derivative - how much output is affected given some change in input ?

So our input \(x\) will go to magic box \(g\) and it will scale, then it will go to magic box \(f\) and will be scaled again
Being that simple, it's slope of \(f\) times slope of \(g\) ?
However if derivative of \(f\), if not static, it will also change with it's input. What`s the input ? \(g(x)\) !

Now we can go back to Hobbiton :)

Gradient descent - revisited

So we know that:

• We want to minimize function \(J_\theta(x)\)
• We can do it by changing the value \(\theta\)
• We need to go in a opposite way of the gradient

Now there is no way around it ! We need derivative of our cost function with respect to \(\vec{\theta}\) !

Derivative of sigmoid

In the cost function, there is sigmoid hidden as it's part of the hypothesis: \(h_\theta(X) = \frac{1}{1+e^{-X\cdot \vec{\theta}}}\)
We will need chain rule to get the whole derivative of \(J\), however let's start with sigmoid

Our goal is get \(\frac{d}{dz} \sigma(z) = \frac{d}{dz} \frac{1}{1+e^{-z}}\)
First, there is reciprocal (\(\frac{1}{f}\)), we know that \((\frac{1}{f})^\prime = \frac{f^\prime}{f^2}\) (you can easily proove it)

Now split it to two parts (we add \(1\) and subtract \(1\) making it still equivalent)

This step is tricky, it took me a lot time to get it, I will try to explain it better... Take some time with this

Graphically it looks like this:

Derivative of cost function

We have

Use chain rule (derivative of logarithm is \(\frac{1}{x}\))

Use chain rule on \(h_\theta(x)\) (it's sigma of \(\theta^\intercal x\))

Now let's take a look at \(\frac{\delta \theta^\intercal x^{(i)}}{\delta \theta_j}\)
It's just sum of products.
Partial derivative with respect to \(\theta_j\) means, that other \(\theta_{i!=j}\) is to be treated as a constant (derivative of constant is zero)
\(\frac{\delta \theta^\intercal x^{(i)}}{\delta \theta_j} = \frac{\delta}{\delta \theta_j} [ \theta_0 \times x_0 + \theta_1 \times x_1 + \dots + \theta_n \times x_n] = (\theta_j)^0 X_j = X_j\)

Let's use this knowledge

We can compact things into single sum

Now let's vectorize it:

Summary

• We went through logistic regression, which is a model for binary classification
• Binary classification is a special case of classification, where there are two classes \(y \in \{1, 0\}\)
• The model with parameters form a hypothesis
• The hypothesis for logistic regression is \(h_\theta(X) = \frac{1}{1+e^{-X\cdot \vec{\theta}}}\)
  • It's a line/hyperplane somewhere in space (position and orientation determined by \(\vec{\theta})\)
  • Points on the decision boundary get's value 0.5
  • Points in one direction gets higher and higher numbers, asymptoticallly approaching 1
  • Points in other direction gets lower and lower numbers, asymptoticallly approaching 0
• If we pick and \(\vec{\theta}\) we can judge how well the hypothesis works with that (how well does it separate the classes of our traning set) using cost function
  • The function is \(J(\vec{\theta}) = \frac{1}{m}[-\vec{y}^\intercal log(h_\theta(X) - (1-\vec{y})^\intercal log(1-h_\theta(X))]\)
  • We call this cost function log loss or binary cross-entropy
• Training the model means picking right value of \(\vec{\theta}\), right value means, that \(J(\vec{\theta})\) is lowest at this point
  • This process is called optimization
  • One of algorithms to do it is gradient descent
  • This algorithm just walks down the landscape to lowest error using small steps / jumps
  • Size of jump is determined by learning rate \(\alpha\)
  • The update rule is \(\vec{\theta} := \theta - \alpha \cdot \frac{1}{m} X^\intercal [h_\theta(X) - \vec{y}]\)
  • We keep walking down the hill, untill we are satisfied or tired

There are infinitely many directions we could go from here - talk about regularization, kernel trick, implementation, vectorized SIMD CPU instructions for linear algebra, talk about different models, cost functions etc.

Right now, I think you deserve to chill like a Hobbit :)

Thank you for reading. If you found an error or better way how to explain something, please contact me on LinkedIn.